Proposition 14.1. Let C be a curve of genus at least two over a number field F . There is a non-torsion cycle ξ in the kernel of the Abel-Jacobi map
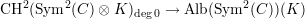
where K is the algebraic closure of the function field F(C).
The conjectures of Bloch and Beilinson mentioned imply that the kernel of the Abel-Jacobi map is torsion when the variety is defined over a number field. In order to see that this conjecture is “tight” we should be able to show that there are cycles of infinite order in this kernel when the field has transcendence degree one.
In joint work with Mark Green and Philip Griffiths we were able to show this in two ways. In the first case we consider the second symmetric power of a curve of genus at least two and we examine the classical Abel-Jacobi map.
Proposition 14.1. Let C be a curve of genus at least two over a number field F . There is a non-torsion cycle ξ in the kernel of the Abel-Jacobi map
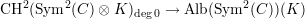
where K is the algebraic closure of the function field F(C).
In the second case, we consider the consider a general surface with non-zero pg and prove this using the étale analogue of the Abel-Jacobi map as defined by Jannsen and Raskind. Let F2CH2(S) denote the kernel of this map.